Chapter 1: Transistors

Transistors are used as basic building blocks in amplifiers. They can also be used as switches.

Bipolar Junction Transistors

The BJT (Bipolar Junction Transistor) is a very common current controlled transistor. A small current flowing through the base ($I_{b}$) allows a much larger current to flow between the collector and the emitter. The amount of current allowed to flow is related to the gain, often shown as $\beta$ or $H_{fe}$, of the transistor. The important formula to remember, with $I_{c}$ the collector current, is:

$I_{c} = \beta\times I_{b}$ , valid when the transistor is operated in its linear mode.

When the transistor is used in its saturated mode (in other words not in linear mode), the collector current will be restricted by the supply voltage and the components (e.g. a resistor) that are connected to the transistor. More of this will follow shortly. Transistors come in all shapes and sizes. The bigger the physical package the larger the possible power dissipation without damaging the transistor. If mounted on a heatsink, even more power can be dissipated. The following picture shows some transistor packages taken from a variety of data sheets.

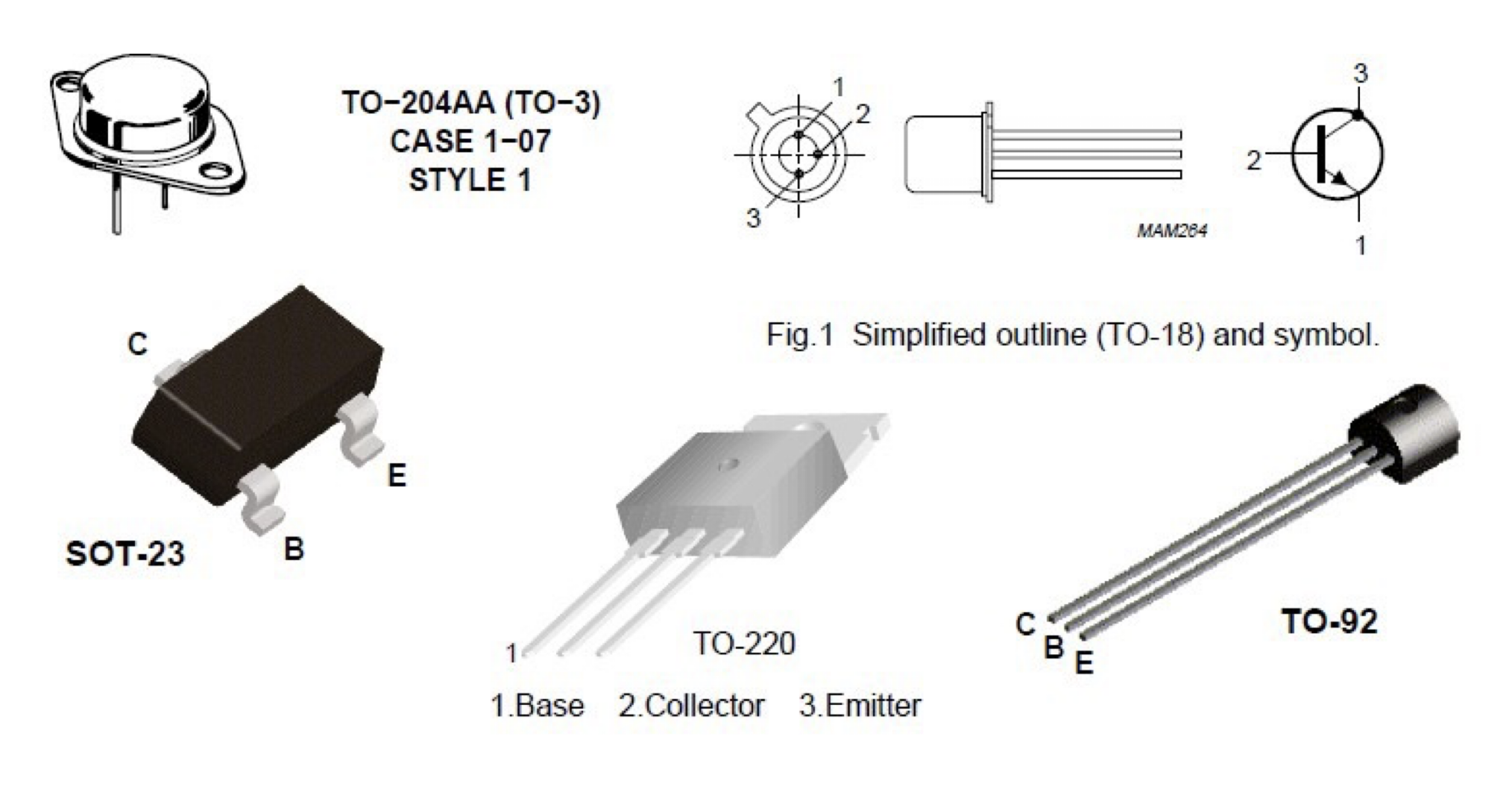Different types of BJT packages showing various sizes and mounting styles Figure 1.1: Different types of BJT packages showing various sizes and mounting styles

The SOT-23 is a very small surface mount package, as can be seen looking at its legs, which are to be soldered on a flat surface. The two types of BJT transistors are NPN and PNP. We will begin discussing the NPN transistor. The emitter is indicated by the arrow in the transistor symbol (see the picture top right above) and shows the direction of current flow, with current direction defined as the flow of positive charge. In the NPN the arrow will point from the base to the emitter. In the picture of the symbol above (top right picture), pin 3 is the collector, pin 2 the base and pin 1 the emitter. In the PNP the arrow will point from the emitter to the base.

NPN transistor: The Saturated Switch Circuit

In the saturated switch application, the transistor is operated like a switch – it is supposed to be either on (when in the figure below $V_{in}$ = HIGH) or off (when $V_{in}$ = LOW). The resistors will have to be designed to ensure saturation. When in saturation mode, it means that the transistor is not operating in its linear mode. The emitter follower, discussed in the next section (4 pages on), is an example of the transistor operating in linear mode.

Current flows through the transistor from collector to emitter in the direction of the arrows. $V_e$ is the lowest voltage in the circuit.

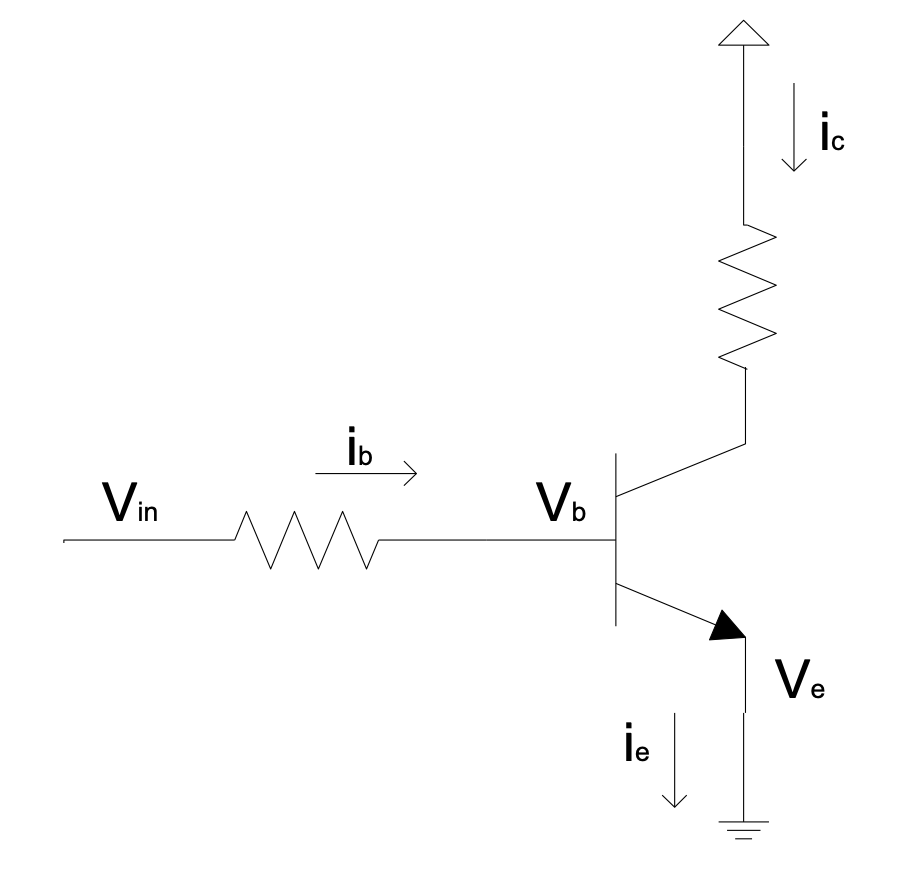Saturated switch circuit with an NPN transistor Figure 1.2: Saturated switch circuit with an NPN transistor

The maximum voltage across the base-emitter junction is about 0.7 V.

$\therefore V_b-V_e\approx \ 0.7 \ V$ , provided $V_{in} >V_{e} + 0.7 \ V$.

This 0.7 V depends on the transistor, a bit on the value of $I_b$, the temperature of the transistor and is an approximate value, but can for most applications be regarded as a constant. The formula also assumes that $V_{in} > V_e + 0.7\ V$ otherwise $V_{be}$ won’t be roundabout 0.7 V.

$i_e=i_c+i_b$ , since it is obeying Kirchoff’s Current Law (KCL).

The transistor has i.e. for small $i_b$ a much bigger $i_c$ will flow. The ratio of $\frac{i_c}{i_b}$ is $\beta$ which is the current gain. A typical specified value of $\beta$ for a 2N3904 transistor is about 100. You are not going to necessarily get this value of $\beta$ in a circuit, as you will see in the next example. Therefore we talk of a specified $\beta$ and an effective $\beta$. We normally run this circuit in “saturated mode”. In this mode the supply voltage can provide enough current $i_c$ so that $i_c$ is limited by the resistance or impedance of the load, not by the transistor. In other words the voltage across the transistor, from the collector to the emitter, will be small.

To illustrate this:

Example 1.1


Suppose we have a 12 $\Omega$ load and a 12 V supply:

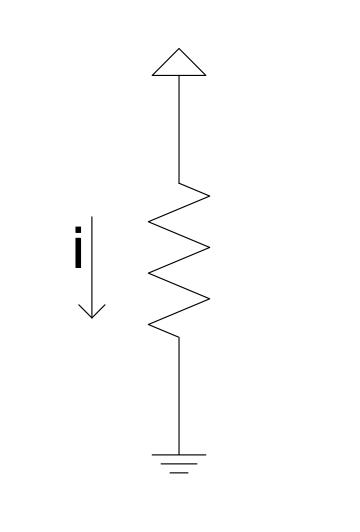Current flowing through a resistor Figure 1.3a: Current flowing through a resistor

By Ohm’s Law:

$$i={V}/{R}=\frac{12\ \mathrm{V}}{12\ \mathrm{\Omega }}=1\ A$$ Take the same load and put it into a transistor switch circuit, with still 12 V at the top:

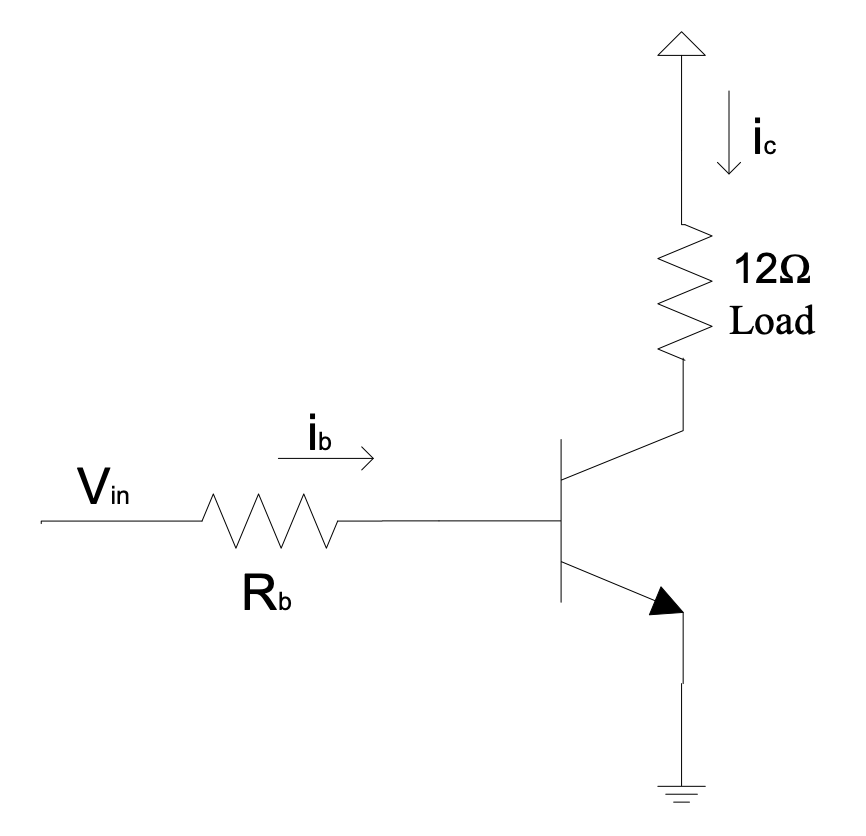Current flowing through a transistor switch circuit Figure 1.3b: Current flowing through a transistor switch circuit

We want to specify the base current so that we allow at least almost 1 A to flow through the load. If we give the base even more current, almost 1 A will still flow through the transistor. It can’t be more because the voltage from collector to emitter can’t be negative in this case (NPN transistor). If we make $R_{b}$ too big, it will cause $I_{b}$ to be too small to ensure almost 1 A in the collector. Then, $$\beta \times I_b< 1\ A,$$ for example 0.8 A. This means $V_{ce}$ will be,

$$12.0 - 0.8\times 12 = 2.4\ V.$$ The effective $\beta$ will be, $$\beta=\frac{0.8 A}{I_{b}}.$$

Depending on the transistor specifications, 0.2 V to 0.5 V is the smallest $V_{ce}$ can be. If the transistor is not saturated, $V_{ce}$ will be bigger because then it will be in the linear mode.

So, with the transistor in saturated mode:

  1. $V_{ce}$ will be roundabout 0.2 V to 0.5 V; and

  2. the effective $\beta$ will be less than the $\beta$ as specified for the transistor in linear mode.

Example 1.2


In the circuit above suppose that the transistor is a TIP31C power transistor. We need a power transistor to handle 1 A loads.

The TIP31C has a minimum (specified) $\beta$ of 25, and a minimum $V_{ce}$ of 0.2 V.

Suppose that $V_{in}$ comes from a microcontroller which guarantees a minimum high level output of 2.4 V. If this output is high, we want maximum current to flow through the load. With low level maximum 0.5 V from the micro, the voltage across the load must be 0 V. What value of $R_b$ should we use?

What is the effective $\beta$ of the transistor now?

Solution:
We require that, $$i_b>\frac{i_c}{\beta} \therefore \ i_b>\frac{1.0}{25} \therefore i_b>0.04\ A$$

Using Ohm’s Law and Kirchoff’s Voltage Law (KVL):

$$i_b={\left(V_{in}-0.7\right)}/{R_b} ={(2.4-0.7)}/{R_b}>0.04$$ $${\therefore R}_b< 42.5\ \Omega$$

In practice the closest standard resistor value $< 42.5\ \Omega$ is 39 $\Omega$ (from the E12 series – see the Appendix), so choose $R_b = 39\ \Omega$. Still assume 12 V at the top.

$\therefore$ the effective gain is,

$$\ \beta =\frac{i_c}{i_b}=\frac{(12-0.2)/12.0}{(2.4-0.7)/39}=22.6$$

Note that the effective value of $\beta$ may be smaller than the given minimum value of $\beta$: it is possible because the design is for the saturation mode. What will happen if we replace the 12 $\Omega$ load with a higher resistance load, like 22 $\Omega$ for example, withoutchanging $R_b$?

The $\beta$ of the transistor will effectively decrease because $V_{ce}$ can’t go smaller than a certain value (like 0.2 V typically). So if the transistor is saturated (very much switched on), thus $V_{ce}$ is the minimum it can be, $\beta$ can effectively be even smaller than theminimum given in the spec sheet of the transistor.

This is possible because the minimum given for $\beta$ in the spec sheet is for the condition of non-saturation or linear mode.

One may even use the effective value of $\beta$ to determine whether the transistor is saturated or not: If the effective $\beta$ is smaller than the minimum of $\beta$ in the spec sheet, the transistor is saturated. Another condition for saturation is that $V_{ce}$ is the minimum it can be.

Question 1.1:

Assuming that $V_{ce}$ can’t be smaller than 0.2 V, calculate the effective $\beta$ in this case (specified $\beta = 25$) if $R_{load} = 22\ \Omega$ and $R_{b} = 33\ \Omega$. A 12 V supply is at the top of the load.

Question 1.2:

Assuming that $V_{ce}$ can’t be smaller than 0.2 V, calculate theeffective $\beta$ in this case (specified $\beta = 25$) if $R_{load} = 5\ \Omega$ and $R_{b} = 33\ \Omega$. A 12 V supply is at the top of the load. Also calculate $V_{ce}$ .

These two questions are significant because they represent working in the two modes of saturation and linear operation respectively.

A standard microcontroller can’t supply 50 mA (0.05 A) from its portpins, so the example circuit above wouldn’t work in practice when trying to drive it directly from a microcontroller. What would be useful is a transistor circuit which gives much higher current gain. The Darlington transistor can help in achieving this.

The Darlington transistor consists of two transistors connected as follows:

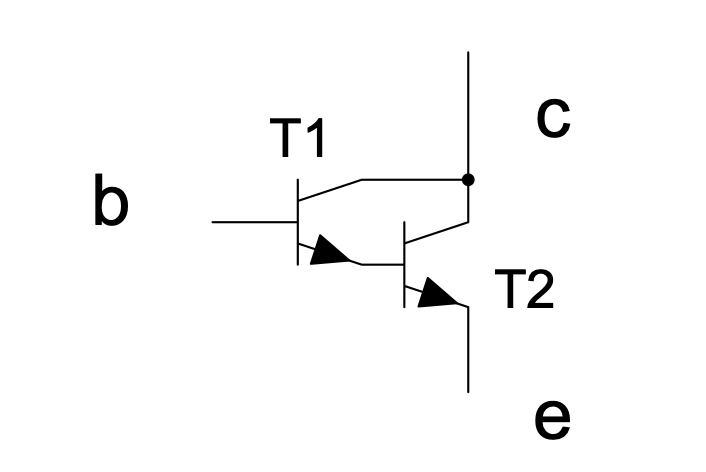Darlington transistor Figure 1.4: Darlington transistor

When we force a current into the base of T1 it causes a current to flow in the emitter of T1. This current goes into the base of T2 which allows a much bigger current to flow in the collector of T2.

The current gain of this circuit will then approximately be the product of the current gains of T1 and T2. T1 can be a low power transistor and T2 a power transistor. T1 only carries T2’s base current. The Darlington transistor has two base-emitter drops in series – thus 1.4 V.

$\therefore V_b-V_e \approx 1.4\ V$, provided $V_{in}>V_{e} + 1.4\ V$, with $V_{in}$ connected to $V_{b}$ through a resistor.

Question 1.3:

Prove that $\beta =\beta_1\left(\beta_2+1\right)+\beta_2\cong \beta_1\beta_2$, for a Darlington in linear mode.

Some Darlingtons incorporate extra base-emitter resistors in order to speed them up.

Question 1.4:

Redo the previous example with the 12 $\Omega$ load, but this time use a TIP122 Darlington with a $\beta> 1000.$ In other words, in the diagram below, the transistor must be replaced by a Darlington transistor. The supply is 12 V and $V_{in} = 2.4\ V$. Determine $R {b}$ (select from the E12 series) and the effective $\beta$.

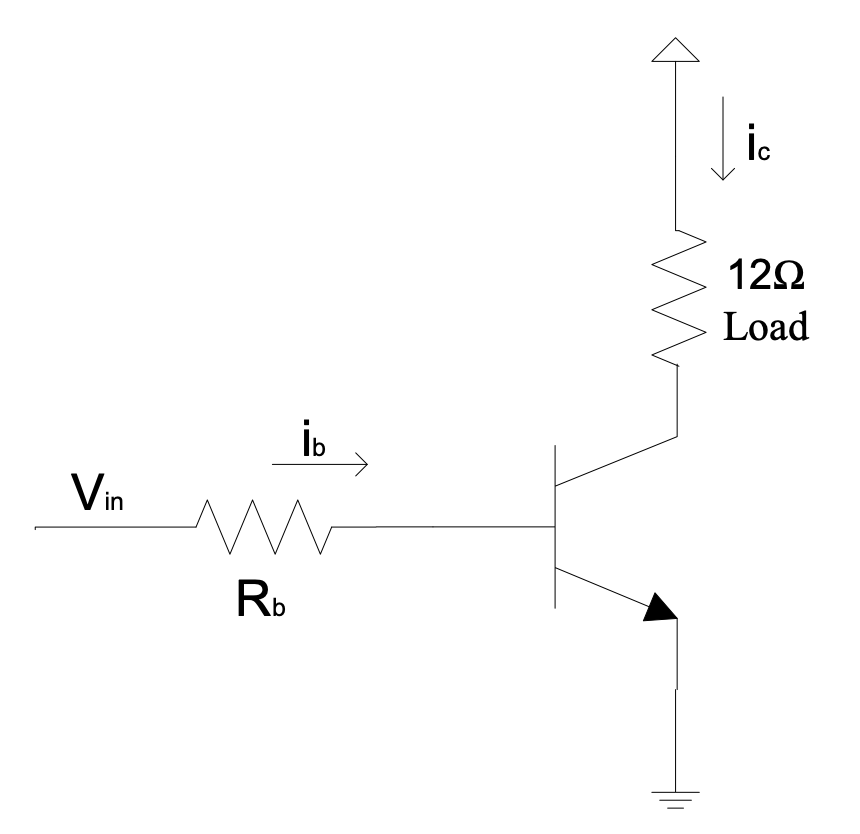BJT transistor replaced by a Darlington transistor Figure 1.5: BJT transistor replaced by a Darlington transistor

$\beta$ is a fairly unreliable figure. It will vary from transistor to transistor of the same type and it will vary with parameters such as temperature. For this reason, you always use the worst-case $\beta$ for your designs. For this same reason you generally only operate this circuit in “digital mode” i.e. the load is either fully on (transistor saturated) or fully off.

NPN transistor: Linear Mode Current Amplification – the Emitter Follower

Some applications require that the voltage across the load is linearly variable. It is useful to be able to control this voltage from a low power signal. In other words we want to control a high power (high current) signal from a low power signal.

The emitter follower circuit (where the load is connected to the emitter, not to the collector as above) does this. The voltage supplied by the emitter to the load is almost the same as the voltage at the base, but much higher current is possible.

In this case the transistor is not saturated, thus it operates in the linear mode.

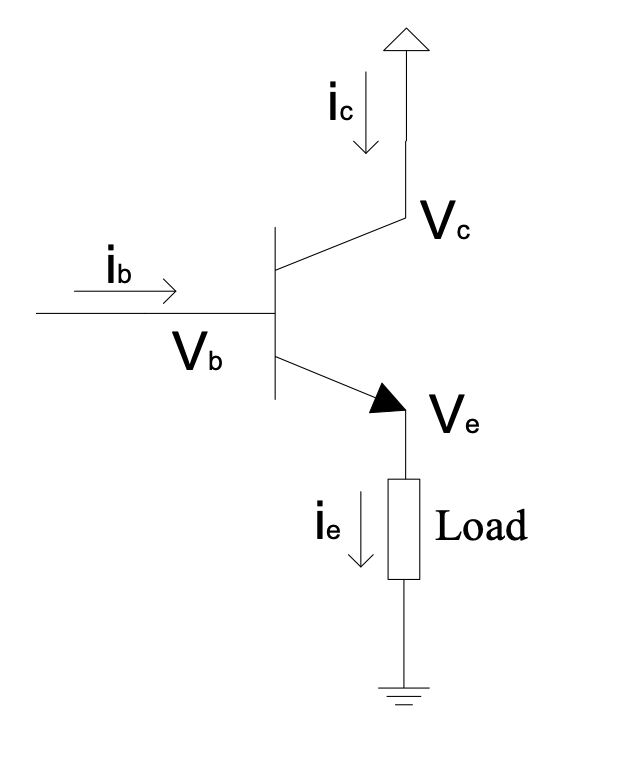Emitter follower circuit Figure 1.6: Emitter follower circuit

As before: $V_e\approx V_b-0.7\ V$

As before: $i_e=i_c+i_b$ and $i_c=\beta i_b$ $$\therefore \ i_e=\left(\beta +1\right)i_b=\frac{\beta +1}{\beta }i_c$$

The important thing to notice in this circuit is that the voltage across the load can be varied linearly by varying the base voltage. In addition we only need a low current into the base to control a much greater current through the load.

By KVL it can be shown that the voltage across the transistor ($V_{ce}$) must vary as the load voltage varies. The transistor takes up the “spare” voltage, such that $V_{supply}=V_{ce}+V_{load}$. $V_{supply}$ is of course fixed and constant.

For electronic devices power P = VI. In this case the power dissipated (as heat) by the transistor is the product of the current through the transistor (which is the same as the current through the load) and the voltage across the transistor ($V_{ce}$), that is

$$P_T=V_{ce}\times i_e.$$

A more accurate equation for the power dissipated in a transistor is:

$$P_T=(V_{be}\times i_b)+(V_{ce}\times i_c)$$

Note that in this formula the collector current is used, not the emitter current. This latter formula can be proven by taking the power in the transistor to be the power provided by the sources to the circuit (the input and the supply) minus the power dissipated in the other components (e.g. the load):

$$P_T=\left(V_b\times i_b\right)+\left(V_c\times i_c\right)-\left(i_b+i_c\right)\times V_e=\left(V_b-V_e\right)\times i_b+\left(V_c-V_e\right)\times i_c$$ $$\ \ \ \ \ \ =(V_{be}\times i_b)+(V_{ce}\times i_c)$$

Example 1.3


For the circuit above when we are using a 10 $\Omega$ load and a TIP31 transistor (with a minimum $\beta$ of 25), 12 V supply and 5 V base voltage:

  1. What voltage is present across the 10 $\Omega$ load?

  2. What current flows in the load?

  3. What current does the 5 V control signal need to provide?

  4. How much power does the transistor dissipate?

Solution:

  1. $5\ V - 0.7\ V = 4.3\ V$

  2. $I = V/R = 4.3/10 = 430\ mA$

  3. If $\beta$ = 25 (minimum): $0.43/(25+1) = 17 \ mA$ (maximum)

  4. $P = VI = (12 - 4.3) \times 0.43 = 7.7 \times 0.43 = 3.31 \ W$, or with the better formula: $P = (V_{be}\times i_b)+(V_{ce}\times i_c) = 0.017 \times 0.7 + (0.43 - 0.017) \times (12 - 4.3) = 3.19 \ W$

As a rough guide – in practice don’t let the TO220 (package of the TIP31) power transistor dissipate more than 1 W without mounting it on a heatsink.

PNP Transistors

PNP transistors allow current to flow through them in the opposite direction to NPN transistors.

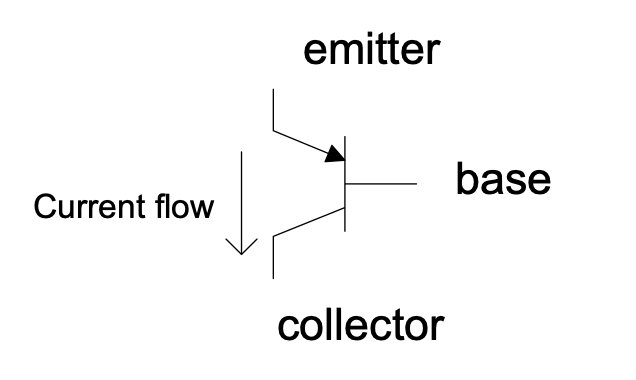Emitter follower circuit Figure 1.7: PNP transistor

For PNP devices the emitter is connected to the highest voltage. Current flows through the device in the direction indicated by the emitter’s arrow, thus it flows out of the collector and out of the base. We can use a PNP transistor to make a saturated switch to control ground-connected loads. Here is such a circuit:

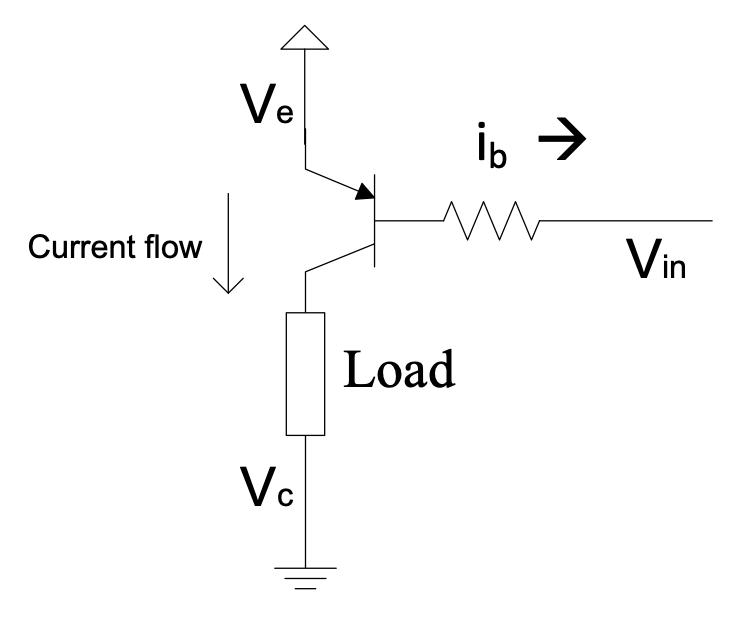Saturated switch circuit with a PNP transistor Figure 1.8: Saturated switch circuit with a PNP transistor

In this case $V_b$ must be 0.7 V than $V_e$.

Requirement: $V_{in}<V_e-0.7$ V for current to flow in the load.

This can be used to turn a load on and off in response to a digital signal have the load and the control ($V_{in}$) sharing a ground.

If needed a resistor can be connected across the emitter and base to alter the switch-on point for $V_{in}.$

We can also make a PNP emitter follower and a Darlington transistor (e.g. TIP127) with PNP transistors. Now with the emitter follower the load is connected between the emitter and the supply voltage:

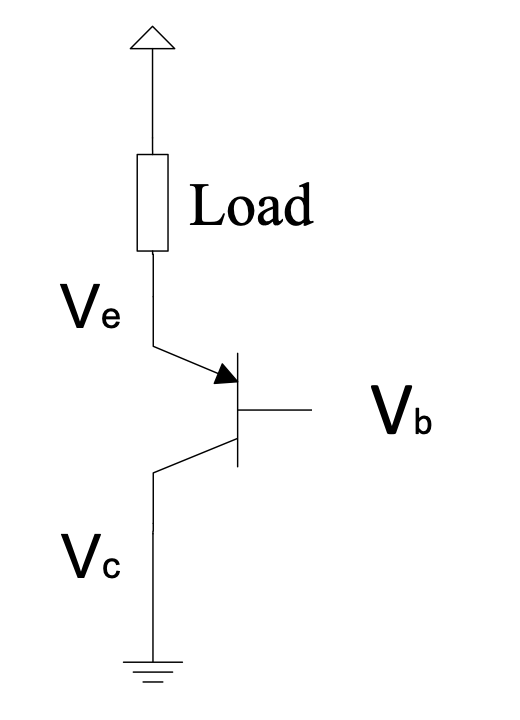PNP emitter follower circuit Figure 1.9a: PNP emitter follower circuit 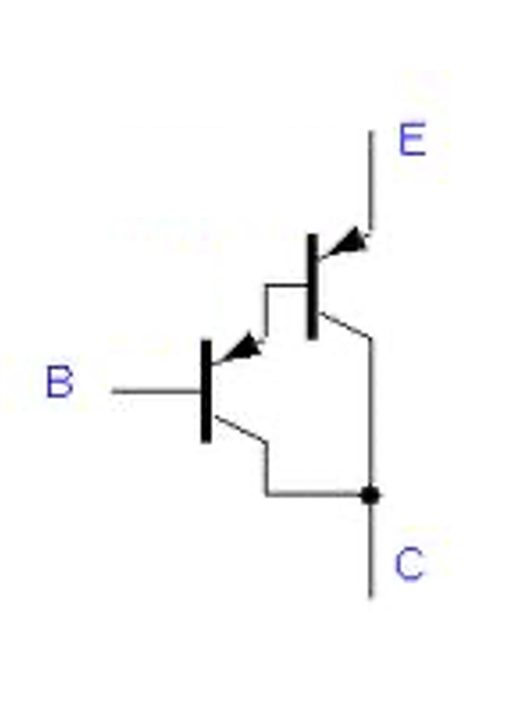PNP Darlington transistor Figure 1.9b: PNP Darlington transistor

Question 1.5:

Why do we need to use a base resistor in the case of the ground-connected load on the previous page, but not necessarily in the case of a supply-connected load?

Bi-directional operation, including H-bridges

With a single transistor (including Darlington) emitter follower we can only actively switch current through the load in one direction. If the load is something such as a DC motor then we may wish to drive it in both directions.

We can combine the NPN and PNP emitter followers to get linear mode bi-directional operation.

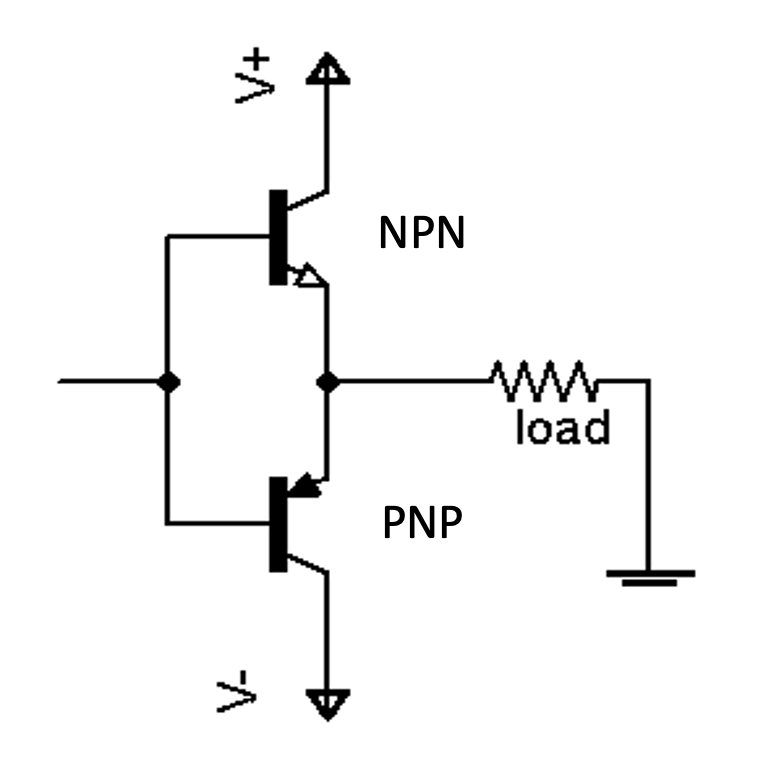The Half-bridge: bi-directional operation with NPN and PNP emitter followers Figure 1.10: The Half-bridge: bi-directional operation with NPN and PNP emitter followers

Note that there will be a deadband in the signal applied to the load if the input is between -0.7 V and +0.7 V. Note that two supplies are required in this case – for the positive and negative supplies.

If we want to run our system off a single supply rail (V- = ground in circuit below) we can combine two of these double-ended emitter followers, therefore configuring an H-bridge.

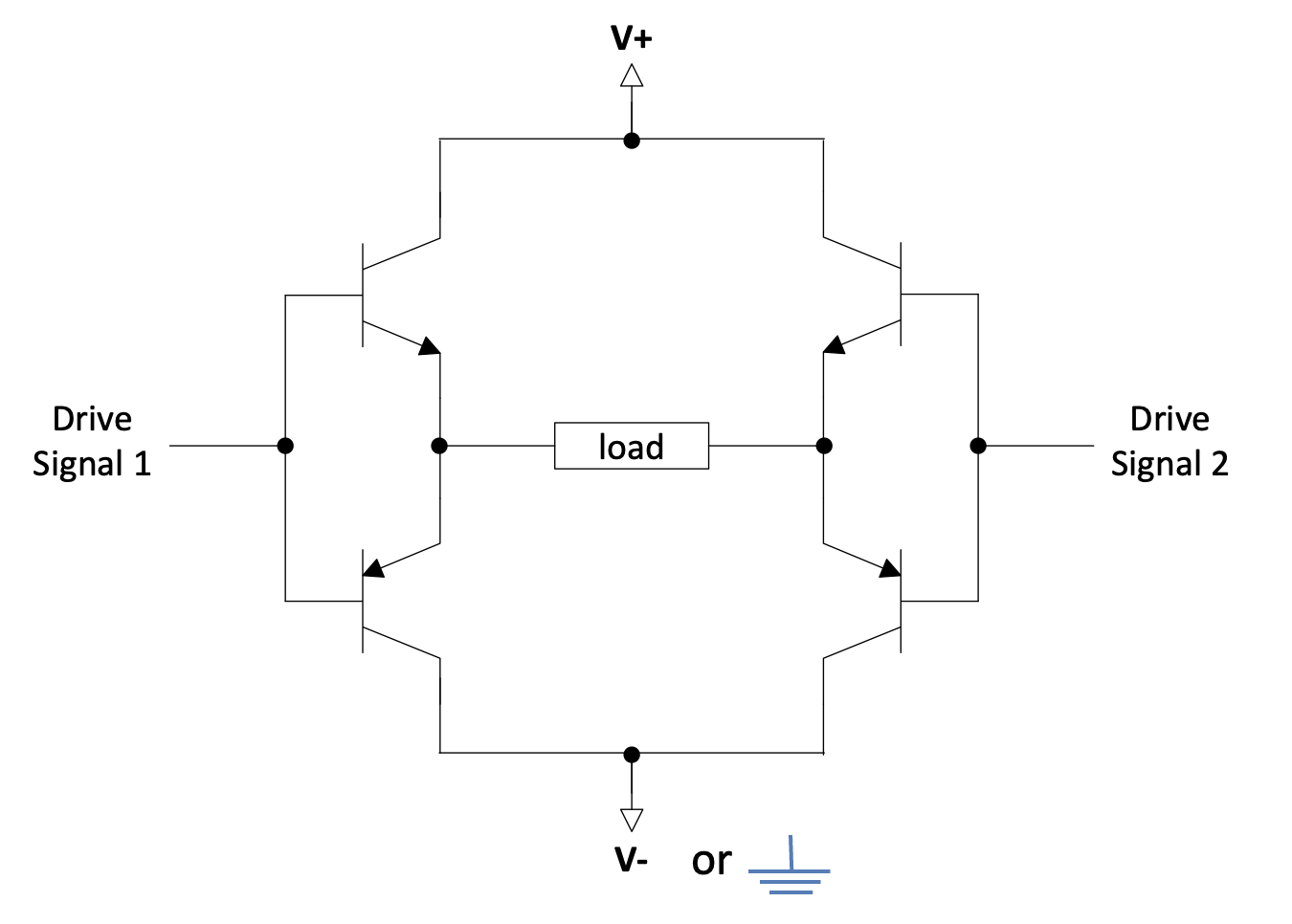The Full-bridge: bi-directional operation with NPN and PNP emitter followers Figure 1.11: The Full-bridge: bi-directional operation with NPN and PNP emitter followers

Drive Signal 1 and Drive Signal 2 are basically driven in anti-phase (if the one is high, the other is low, and vice versa, but there are exceptions – see further on). Their levels will typically be possible to vary between about $V^{+}$ and $V^{-}$. $V^{-}$ may of course be zero (ground) in this circuit. Then Drive Signal 1 and 2 will have to vary around the value $\frac{V^{+}}{2}$.

A disadvantage of this H-bridge, especially if Darlingtons are used instead of transistors, is that the maximum possible voltage across the load is quite a bit less than $V^{+} - V^{-}$. It is about ($V^{+} - V^{-} - 2 \times 0.7$) in the case of transistors and ($V^{+} - V^{-} - 2 \times 1.4$) in the case of Darlingtons, if the Drive Signals have extreme values of $V^{+}$ and $V^{-}$. It is important that you understand why the maximum possible voltage across the load is not for example ($V^{+} - V^{-} - 2 \times 0.2$).

It is probably not a good solution to solve this by letting the Drive Signals have larger voltage levels than the H-bridge supply, because this will require extra supplies. The problem of deadband will also be present in this emitter follower H-bridge when used in the linear mode. Using the H-bridge in saturated mode only, will be when the Drive Signals are designed to be only as close as possible to $V^{+}$ or to $V^{-}$ ; not any other voltage in between.

Therefore, the following is a better H-bridge configuration, but now resistors are required between the drive signals, the supply voltages and the transistor bases. Note that the NPN and PNP transistors have been swopped.

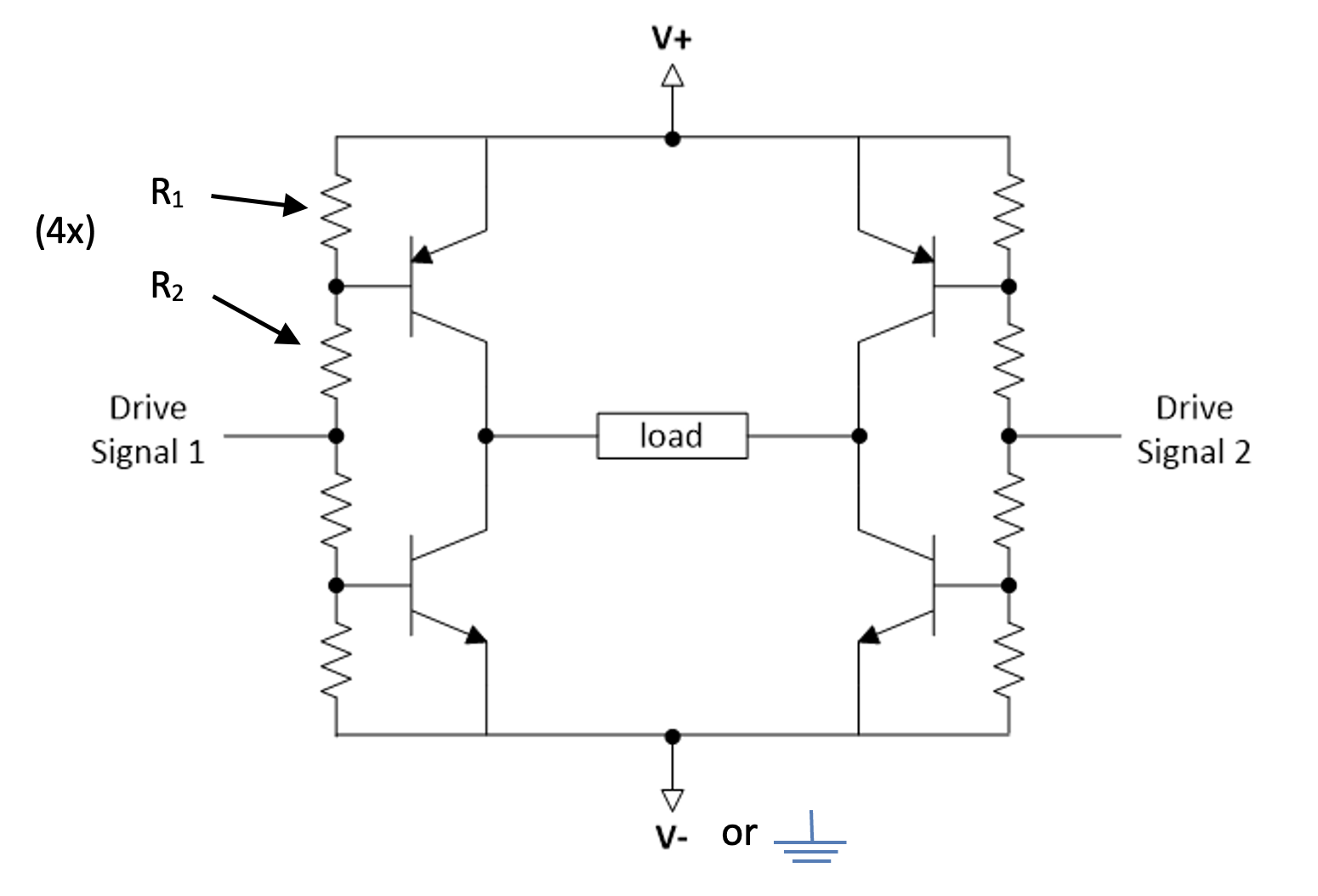The PNP driven H-bridge configuration Figure 1.12: The PNP driven H-bridge configuration

Question 1.6:

Why can’t the Drive Signals be directly connected to the bases such as with the emitter follower H-bridge?

Whereas the emitter follower H-bridge can be used in the linear or saturated mode, the last H-bridge is only well-suited for the saturated mode, such as when driving it with a PWM signal (Pulse Width Modulated, see below).

Resistors are also required in the last H-bridge between the base and emitter pins of each transistor or Darlington to prevent high current to flow straight from the top to the bottom transistor in any of the legs of the H-bridge. This may occur:

  1. when the drive signal is momentarily halfway between $V^{+}$ and $V^{-}$ while switching from $V^{+}$ to $V^{-}$ or vice versa (not necessarily a problem because the switching may be fast enough), or

  2. when the drive signals are not connected for testing purposes or by accident.

Therefore the resistors must be designed such that if the Drive Signal = $\frac{V^{+} + V^{-}}{2}$, the voltage between the emitter and base must be less than 0.7 V in the case of a transistor, and less than 1.4 V in the case of a Darlington. (0.5 V and 1.0 V are respectively recommended.) Also, if the Drive Signal = $V^{-}$, only the top transistor or Darlington must be fully switched on, and if the Drive Signal = $V^{+}$, only the bottom transistor or Darlington must be fully switched on.

Keep also in mind that there must be sufficient base current so that the required current to the load can be supplied.

The maximum possible voltage across the load is still a bit less than $V^{+} - V^{-}$, but it should be better than with the emitter follower H-bridge.

It is about ($V^{+} - V^{-} - 2 \times 0.5$) if we assume that $V_{ce}$ (saturated) is 0.5 V, if the Drive Signals have extreme values of $V^{+}$ and $V^{-}$.

Question 1.7:

If $V^{+} = 12.0\ V$ and $V^{-} = 0.0\ V$, assuming the levels of the Drive Signals are also $V^{+}$ or $V^{-}$, and Darlingtons with $\beta = 1000$ are used, show that the 8 resistors in the H-bridge can be four 180 $\Omega$ ($R_{1}$) and four 1.0 k$\Omega$ ($R_{2}$ resistors. Also show that a load of 5 $\Omega$ can be driven by this amplifier.

Be careful; if a different supply voltage is used, or if a smaller load resistance must be driven, the resistors must be redesigned. But the design will work for the same supply but a bigger load resistance.

PWM (Pulse Width Modulation)

A PWM signal may be generated by electronically comparing a signal with a triangular wave. This is demonstrated below.

The big advantage of PWM is that less heat is generated, or power wasted, in the amplifier transistors, because the transistors are only fully on or fully off. If they are fully on, the voltage across them is low, therefore although the current is high, the power dissipated in the transistors is low. If they are fully off, the current through them is very low, although the voltage across them is high, therefore the power dissipated in them is again low.

A comparator generating a PWM signal, can be explained as follows:

  1. If the signal is bigger than the triangular wave, the PWM signal has a high value.

  2. If the signal is smaller than the triangular wave, the PWM signal has a low value.

The triangular wave is usually of much higher frequency than the bandwidth (highest frequency) of the signal that must be converted to a PWM signal.

Example signals:

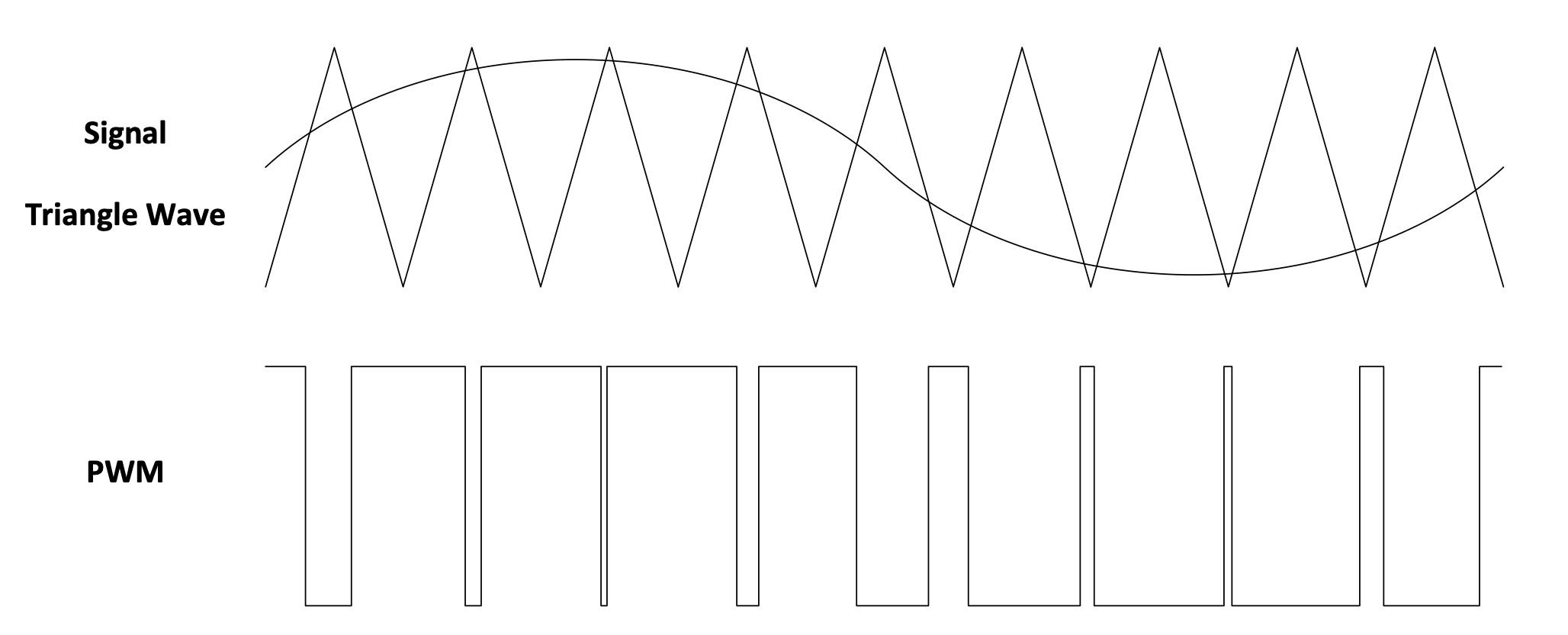Example PWM signal Figure 1.13: Example PWM signal

On average, or low-pass filtered, the PWM signal is just the same as the original signal.

The duty cycle of a PWM signal is the ratio of the time the signal is high to the period of the triangular wave. If the duty cycle is constant, the period of the repeating PWM signal will be equal to the period of the triangular wave. This is important to know because the triangular wave will not always be visible (or even exist depending on how it was generated).

The duty cycle of the PWM signal changed from almost 100% to almost 0% in this example. With a duty cycle of 50% the average will be halfway between the maximum and the minimum of the PWM signal.

The reason why less power is dissipated in the transistors of the amplifier driven with a PWM signal compared to a continuous signal, is that when high current is flowing through the transistor, the voltage across the transistor is low, and when the voltage across the transistor is big, the current through it is very small. Therefore P = VI for the transistor stays small.

H-bridges may be driven with two possible PWM schemes:

  1. The first PWM scheme is to control Drive Signals 1 and 2 to be always out of phase, with one Drive Signal equal to the PWM signal (though signal conditioning may be necessary), and the second Drive Signal the inverse of the first. Then 50% duty cycle will correspond with 0 V DC across the load on average, 0% will correspond with maximum negative voltage and 100% with maximum positive voltage across the load.

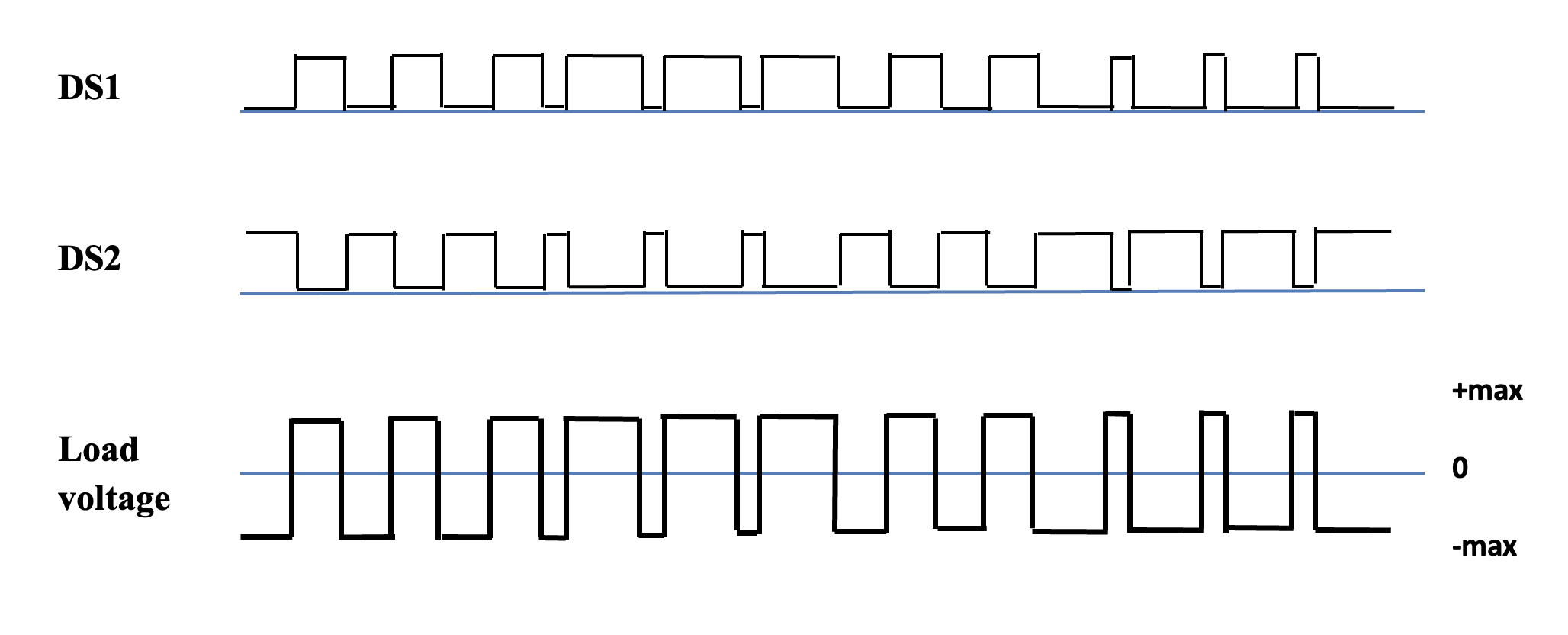The first PWM scheme: DS1 and DS2 out of phase Figure 1.14: The first PWM scheme: DS1 and DS2 out of phase

  1. The second PWM scheme is to control one Drive Signal with the PWM signal or its inverse* (signal conditioning may be necessary) and to let the second Drive Signal be either positive or negative depending on the required sign of the voltage across the load. Then 50% duty cycle will correspond with half the maximum positive voltage across the load if the sign is positive, but 50% duty cycle will correspond with half the maximum negative voltage across the load if the sign is negative. *The inverse will be necessary if the sign is changed, because 0% duty cycle with one sign will mean 100% duty cycle with the other sign. To explain this: Say e.g. DS2 is low just before the sign change. DS1 is mostly low because the load voltage is close to zero. If the load voltage must now change to a small negative value, DS2 must go high. Then DS1 can’t stay mostly low, because this will cause a large negative voltage across the load. Therefore the PWM signal to DS1 must be inversed.

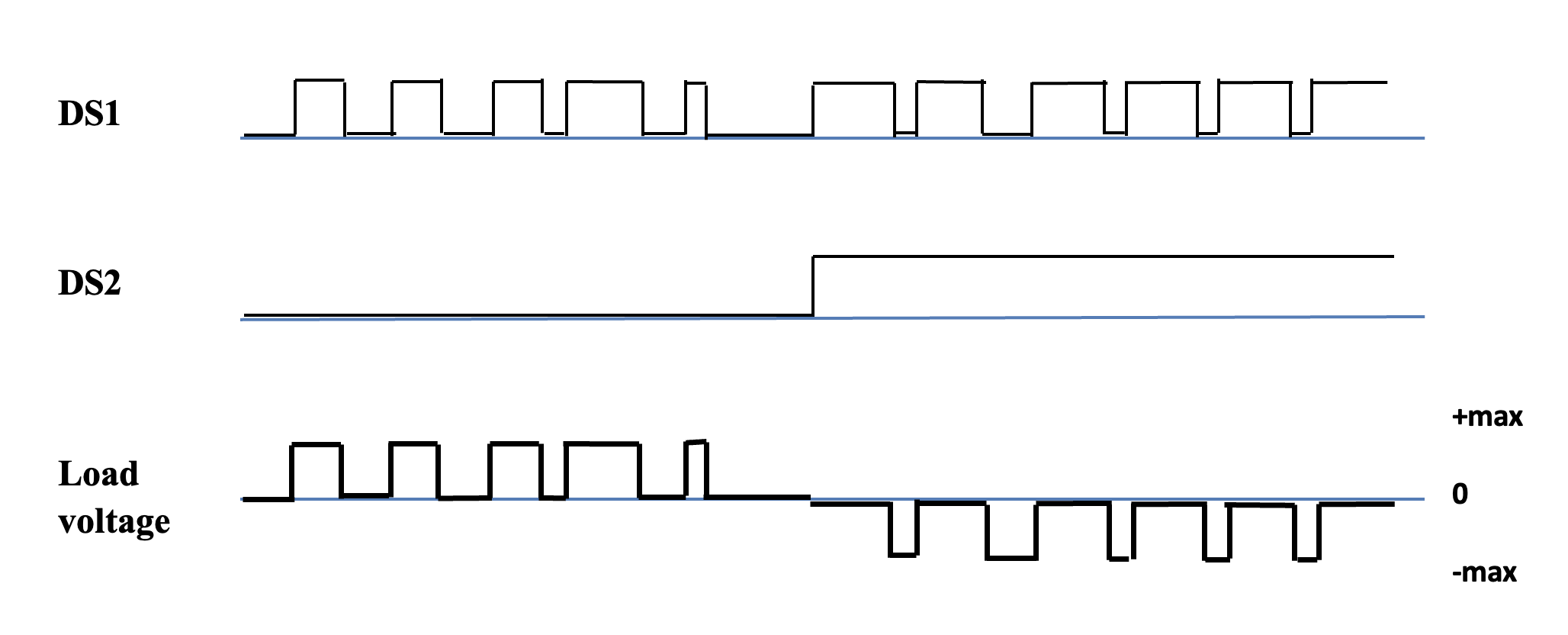The second PWM scheme: DS1 (or DS2) driven by a PWM signal with the other acting as a direction signal Figure 1.15: The second PWM scheme: DS1 (or DS2) driven by a PWM signal with the other acting as a direction signal

The second scheme will require more code if the PWM is generated in a micro-processor, but the resolution will be double that of the first scheme. PWM controller chips can be found that do all of these, but you must understand how it works to use it best.

Current Sources

Some loads produce an effect related to the current that is driven through them. Examples include:

  1. LEDs: The light output is related to current

  2. Motors: (DC) Torque is proportional to current

  3. Heating elements: Some applications require constant current to be used

A circuit which drives a constant current through the load, independent of the load (up to certain limits), is called a “constant current source” or “current source”. Depending on the direction of the current through the load it may also be called a “current sink”.

Below is a simple current source (actually current sink) circuit:

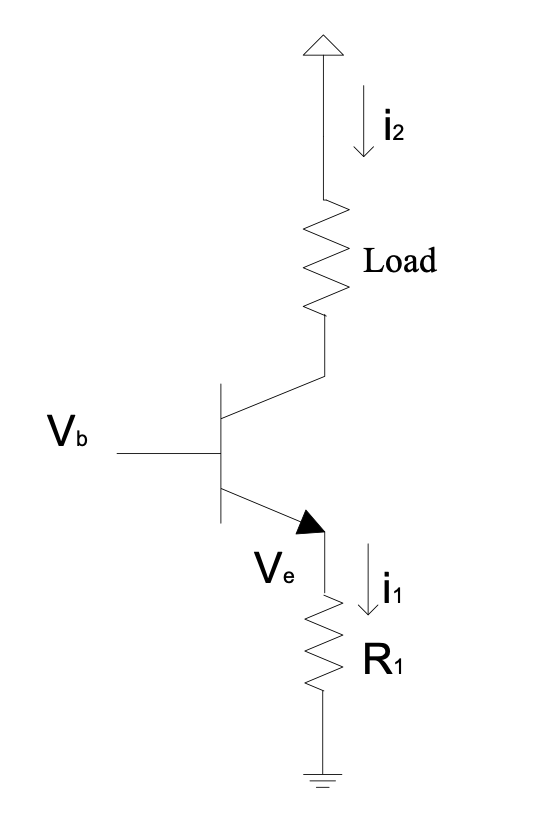
Simple current source circuit
Figure 1.16: Simple current source circuit

Here: $V_e=V_b-0.7$ V and $i_1=\frac{V_e}{R_1}=\frac{V_b-0.7}{R_1}$

For high $\beta$ transistors $i_1\approx i_2$ (because $i_1=\frac{\beta_1+1}{\beta_1}i_2$) $$\therefore i_2\approx \frac{V_b-0.7}{R_1}$$ The current in the load $i_2$ , is not affected by the load’s resistance. As the load resistance changes, the voltage across it automatically changes to compensate.

There is a limit to this: The sum of the voltage across the emitter resistor, the voltage across the load and the saturation voltage of the transistor can never be greater than the supply voltage. The maximum voltage which the current source can put across the load is called the “compliance” of the source.

If the supply voltage changes then the current through the load will also be constant, although the compliance will be reduced when the supply drops, or will be increased when the supply increases.

This is called a voltage controlled current source because the current through the load is determined by the voltage $V_{b}$.

Question 1.8:

Give the more accurate formula for $i_2$ as a function of $V_{b}$, $R_{1}$ and $\beta$(in other words don’t assume that $\beta$ is necessarily very high).

Give the accurate formula for $i_2$ if $R_{1}$ is moved from the emitter to the base.

Why is this latter case a worse current source compared to the previous case?

Voltage Amplification

We can use a transistor’s current amplification to produce voltage amplification. Consider the following circuit:

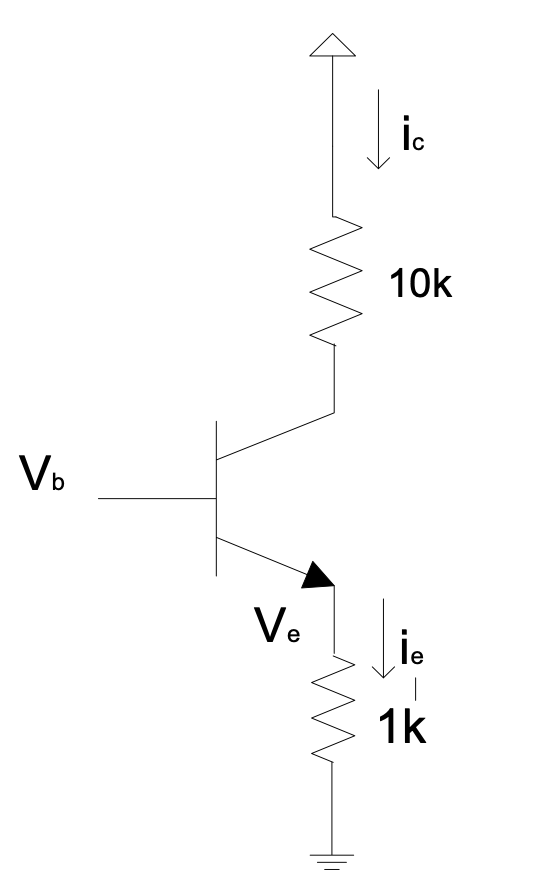Voltage amplification circuit Figure 1.17: Voltage amplification circuit

For $V_b = 1.7\ V$: $V_e = 1\ V$ and $i_e = 1 mA$. Therefore $i_c$ will be approximately 1 mA.

By Ohm’s Law, the voltage across the collector resistor is 10 V.

If we increase $V_b$ by 1 V, thus to 2.7 V, the voltage across the collector resistor will then be 20 V.

Again the combination of the supply voltage and the saturation voltage of the transistor will be a limiting factor.

From this we see that the voltage on the collector has changed by 10 V in response to a 1 V change in the input signal. The gain of this circuit is determined by the ratio of the resistors. This is not very accurate as various transistor effects tend to reduce gain.

Much more accurate results are possible with Operational Amplifiers – to be discussed in Chapter 2.

Question 1.9:

With $V_{s}$ the supply voltage, $V_{b}$ and $V_{c}$ the base and collector voltages, and $R_{c}$ and $R_{e}$ the resistors connected to the collector and the emitter:

  1. Derive $\frac{V_s-V_c}{V_b-0.7}$ in terms of $R_{c}$, $R_{e}$ and $\beta$.
  2. Derive the minimum and maximum $V_{b}$ may be, in terms of $V_{s}$, $R_{c}$, $R_{e}$ and $\beta$ for the formula above to be still valid, with $V_{ce}$ minimum assumed to be 0.2 V.

Answer b): $0.7<V_b<0.7+\frac{V_s-0.2}{1+\frac{\beta }{\beta +1}.\frac{R_c}{R_e}}$

Field Effect Transistors

N-channel, P-channel, Enhancement Mode, Depletion Mode

The FET (Field Effect Transistor) is a common voltage controlled transistor. With FETs we talk of drain, gate and source for its 3 terminals, not of collector, base and emitter as with BJTs. A voltage between its gate and its source ($V_{GS}$) allows a large current to flow between the drain and the source. The amount of current allowed to flow is related to the forward transconductance, often identified as $g_{FS}$(in A/V or S for siemens, or mho coming from ohm in reverse). $V_{GS}$ must exceed a threshold value ($V_{GS(th)}$, in V) before drain current will flow. The important formula to remember, with $I_{D}$ the drain current, is:

$I_{D}$ = ($V_{GS}$ – $V_{GS(th)}$) $g_{FS}$, valid when the transistor is operated in its linear mode.

When the transistor is used in its saturated mode, the drain current will be restricted by the components (e.g. a resistor) that are connected to the transistor.

The JFET (Junction Field Effect Transistor) was first developed, and was later mostly superseded by the MOSFET (Metal-Oxide Semiconductor Field Effect Transistor). Many more types of FETs are found, but all won’t be discussed or used in this course.

The MOSFET has very large input impedance, in other words the gate current is very low.

$\therefore I_S=I_D$ is a valid approximation, with $I_S$ the source current.

Similar to NPN and PNP BJTs, one also gets N-channel and P-channel FETs. As in BJTs where the direction of the current flow in NPN and PNP is opposite, in FETs the direction of the current flow in N-channel and P-channel is also opposite.

The last subtypes I would mention here are the Enhancement Mode and Depletion Mode MOSFETs. The blocked formulas above are applicable to both these subtypes, but the difference lies in $V_{GS(th)}:$

  • Enhancement Mode N-channel: $V_{GS(th)}$ is positive with $V_{GS} = 0\ V$ switching the transistor off and $V_{GS}$ $>$ $V_{GS(th)}$ switching it on.

  • Enhancement Mode P-channel: $V_{GS(th)}$ is negative with $V_{GS} = 0\ V$ switching the transistor off and $V_{GS} < V_{GS(th)}$ switching it on.

  • Depletion Mode N-channel: $V_{GS(th)}$ is 0 V with $V_{GS} < 0\ V$ switching the transistor off and $V_{GS} > 0\ V$ switching it on.

  • Depletion Mode P-channel: $V_{GS(th)}$ is 0 V with $V_{GS} > 0\ V$ switching the transistor off and $V_{GS} < 0\ V$ switching it on.

These are the symbols of N-channel and P-channel enhancement mode MOSFETs:

N-channel and P-channel enhancement mode MOSFETs 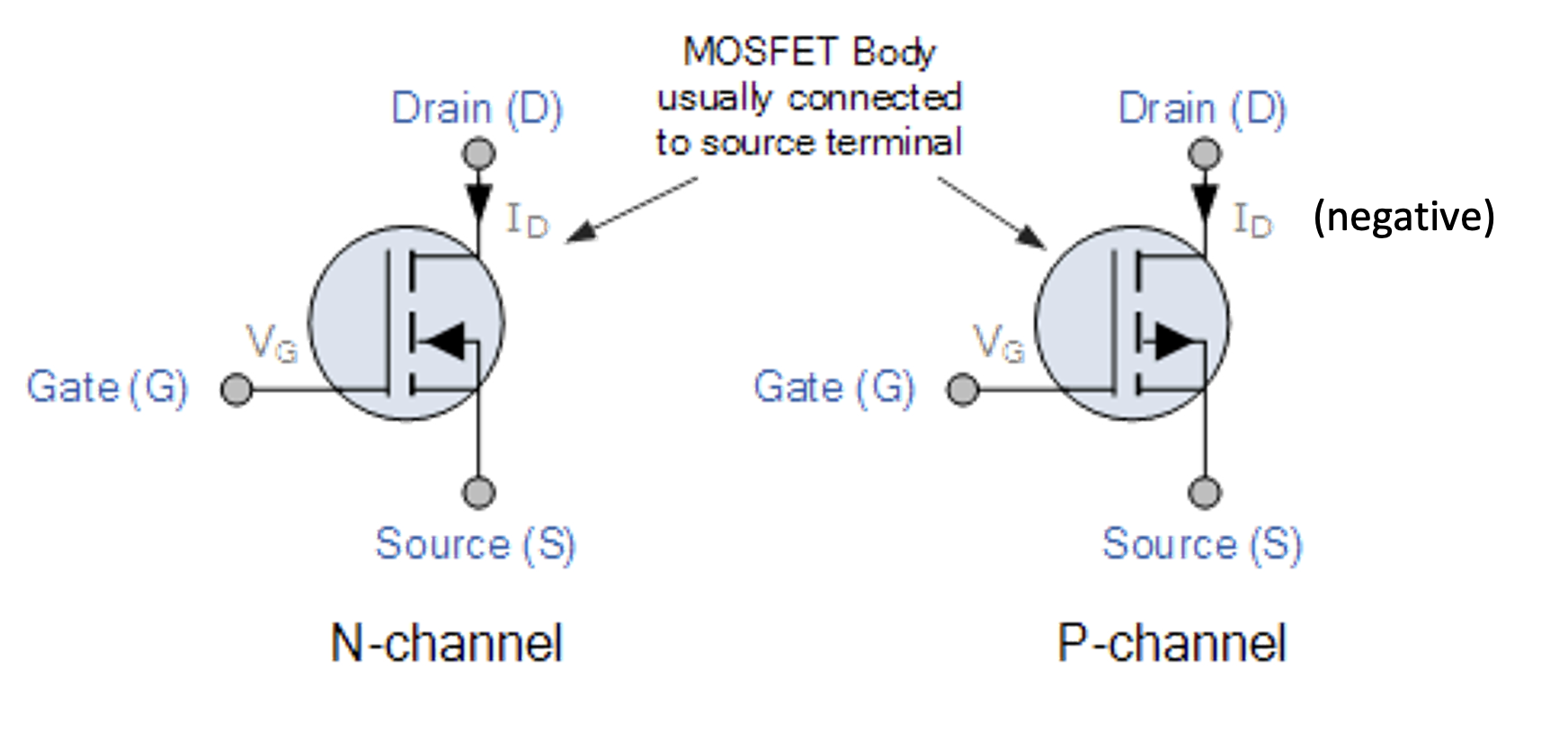Figure 1.18: N-channel and P-channel enhancement mode MOSFETs

For a P-channel, the arrow in the symbol is turned around, and for depletion mode, the dashed lines will be solid. Although the current is still shown here to flow from drain to source for the P-channel, in datasheets the current will be specified as negative, so the current will actually flow from source to drain. So a positive supply will be connected to the source, and the load will be connected between the drain and ground.

These are the symbols of N-channel and P-channel depletion mode MOSFETs:

N-channel and P-channel depletion mode MOSFETs 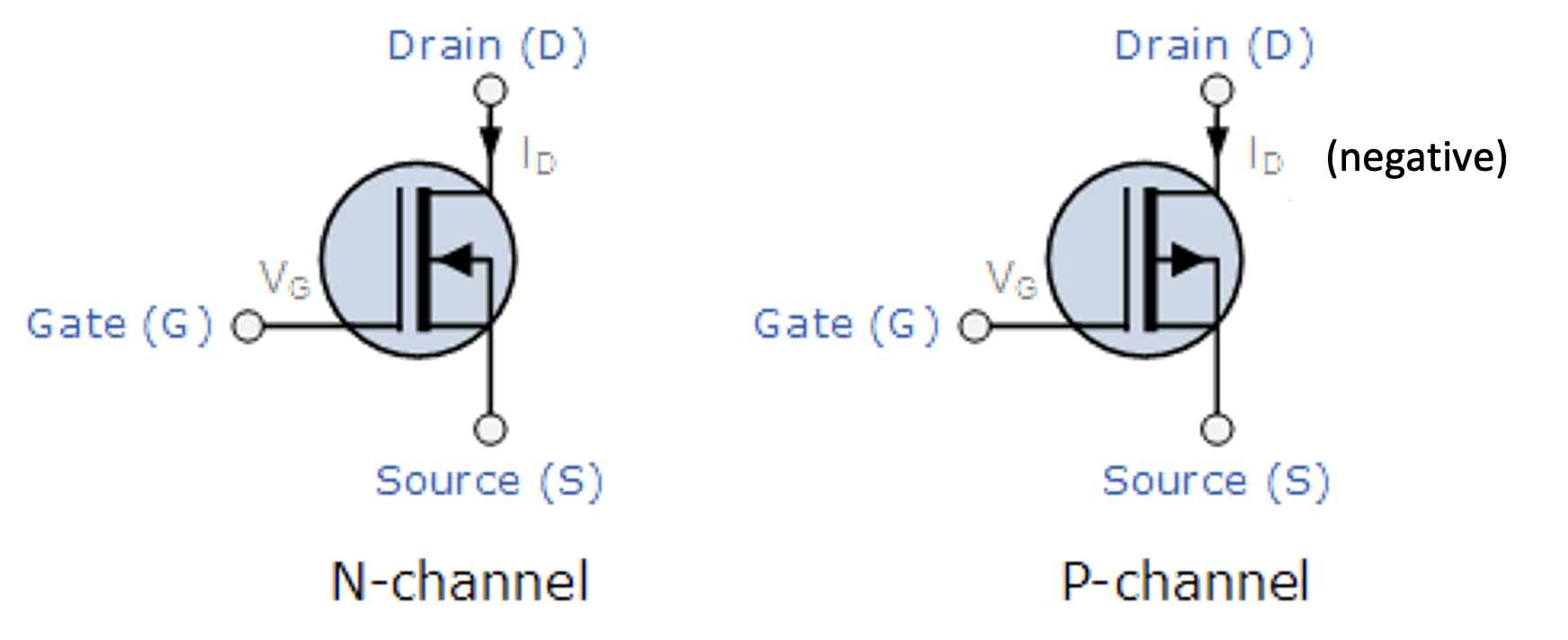Figure 1.19: N-channel and P-channel depletion mode MOSFETs

Again $I_{D}$ as shown here with the P-channel, will be negative.

Examples 1.4


If an N-channel MOSFET with threshold voltage of 2 to 4 V is to be used in saturated mode, with the load connected between a positive supply and the drain, and the source of the MOSFET connected to ground, $V_{GS} < 1.0\ V$ will have it switched off completely, and $V_{GS} = 10\ V$ will have it switched on completely.

If an N-channel MOSFET is to be used in saturated mode, with the load connected between a positive supply and the drain, and the source of the MOSFET connected to ground, typically $V_{GS} < -2.0\ V$ will have it switched off completely, and $V_{GS} = 5\ V$ will have it switched on completely.

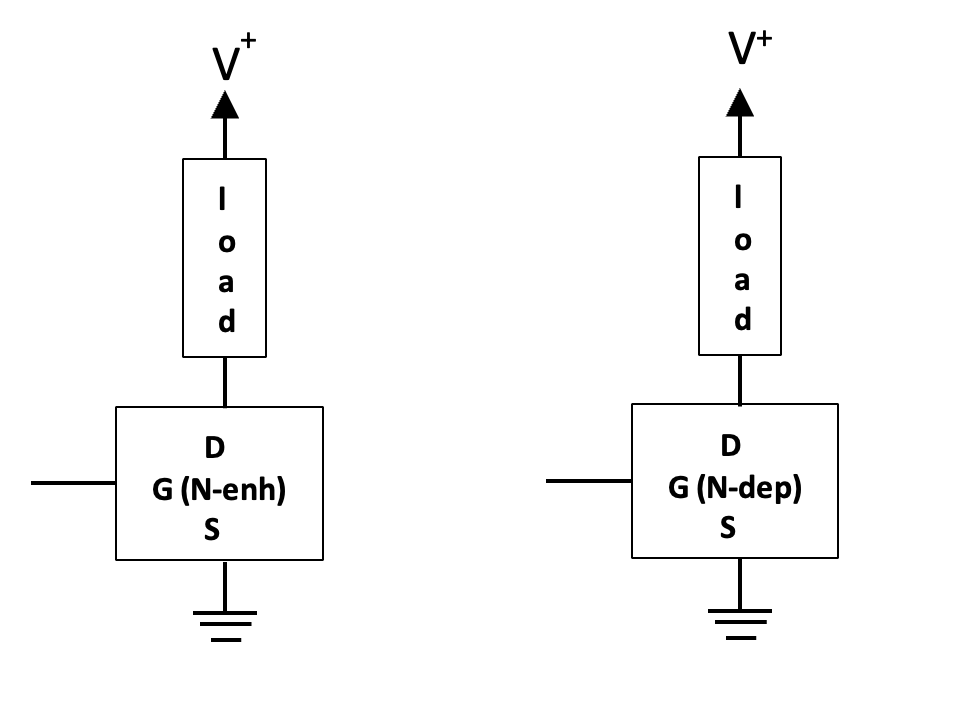MOSFETs in a saturated switch circuit Figure 1.20: MOSFETs in a saturated switch circuit

It is fine to indicate FETs as in this diagram, whenever hand drawn

FETs in an H-bridge

H-bridges can also be designed with MOSFETs, especially enhancement mode MOSFETs as in the circuit below.

Parts list:

  • Q2, Q4, P-channel MOSFET IRF9630 (6.5 A, 200 V)
  • Q1, Q3, N-channel MOSFET IRF630 (9 A, 200 V)
  • Q5, Q6, 2N2222A NPN bipolar transistor

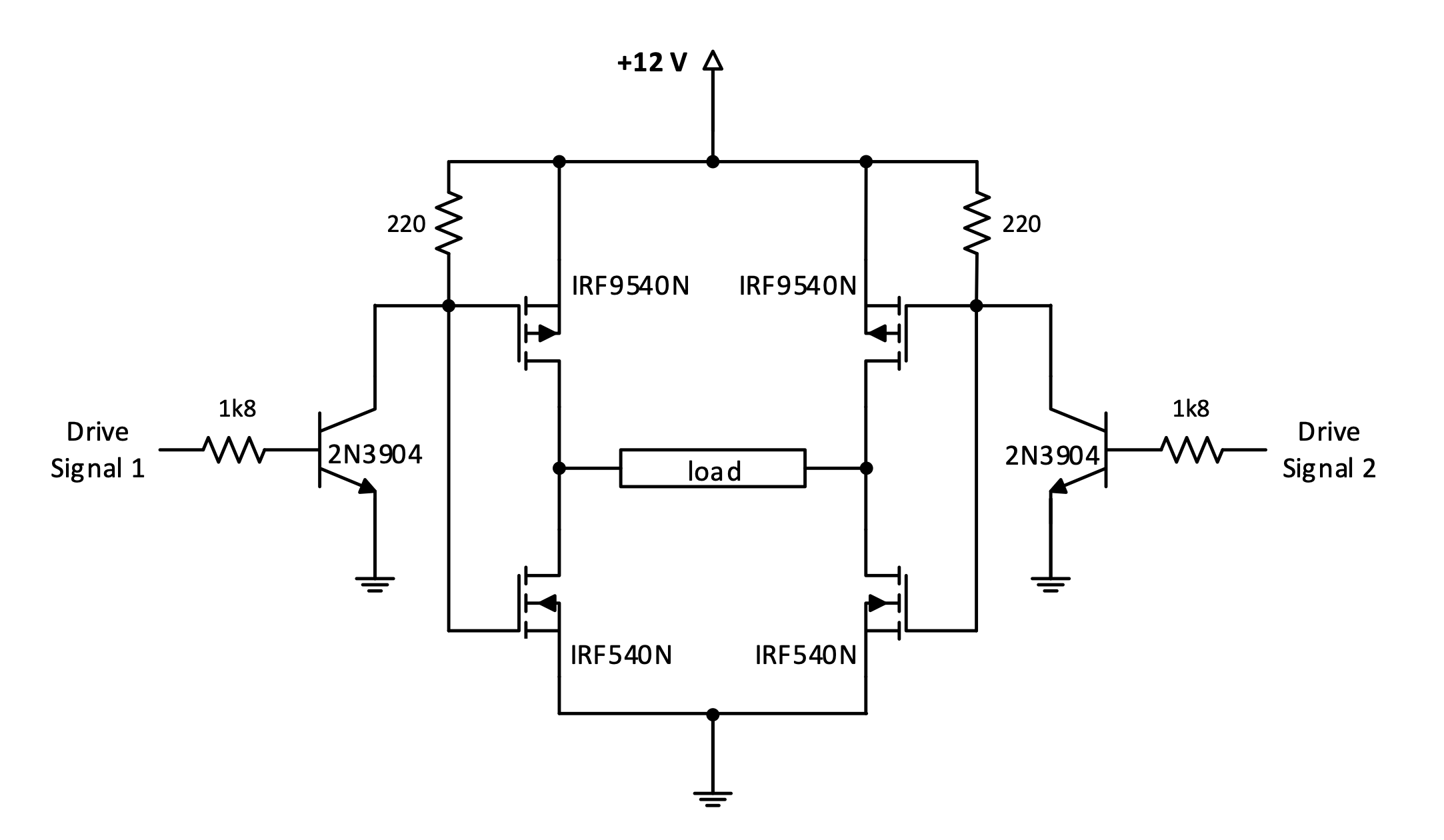MOSFET H-bridge circuit using enhancement mode MOSFETs Figure 1.21: MOSFET H-bridge circuit using enhancement mode MOSFETs

It is easy to design these resistors, because the Gate current here is so small, it can be neglected. Therefore, the resistors can also have much higher values, saving current from the supply. Except if higher switching speeds are required – the next circuit is an example of this.

This scheme of controlling the Gates of the FETs can’t be used with BJT or Darlington H-bridges in saturated mode, because the bases of the latter can’t be connected together since this will cause the transistors on one side of the load to be on at the same time.

In practice it seems to be very hard to find P-channel and N-channel FETs that have good complementary characteristics. But the design can often work even though the characteristics are not exactly complementary, as in the given circuit.

The potential problem of this circuit is also that at the switching moment when the collector of Q5 or Q6 is sitting at 6 V, the FETs above and below on the same side of the motor will both be switched on, causing a current spike from the 12 V supply to ground through Q2 and Q1 or through Q4 and Q3. In practice it seems that this is not a problem, probably because the Gate signals switch fast enough.

We shall return to level adjusters in the next chapter, but they are required between the drive signals and the H-bridges if the drive signals don’t have voltage levels equal to the supply voltages of the H-bridges. Each BJT and the two resistors connected to it, form a level adjuster. Compared to the saturated mode Darlington H-bridge, where more complex level adjusters are required, this MOSFET H-bridge has the following advantages:

  1. Wider range of supply voltages

  2. Wider range of load currents

  3. Less voltage drop over the transistors, therefore less heat loss in the transistors

  4. Faster switching, therefore it can handle higher PWM frequency

  5. Less components